Advertisements
Advertisements
प्रश्न
A square is inscribed in a circle. Find the ratio of the areas of the circle and the square.
उत्तर
Let the side of the square be a and radius of the circle be r
We know that if a circle circumscribes a square, then the diameter of the circle is equal to the diagonal of the square.
`∴ sqrt(2a) = 2r`
`⇒ a = sqrt(2r)`
Now ,
`"Area of circle"/"Area of square" = (pi"r"^2)/"a"^2`
`= (pi"r"^2)/(sqrt(2r))^2`
`= ( pi"r"^2)/(2pi^2)`
`= pi/2`
Hence, the ratio of the areas of the circle and the square is π : 2
APPEARS IN
संबंधित प्रश्न
A lawn is in the form of a rectangle whose sides are in the ratio 5 : 3. The area of the lawn is `3375m^2` . Find the cost of fencing the lawn at ₹ 65 per metre.
Two circular pieces of equal radii and maximum area, touching each other are cut out from a rectangular card board of dimensions 14 cm × 7 cm. Find the area of the remaining card board. (Use π = 22/7).
In the following figure, there are three semicircles, A, B and C having diameter 3 cm each, and another semicircle E having a circle D with diameter 4.5 cm are shown. Calculate:
(i) the area of the shaded region
(ii) the cost of painting the shaded region at the rate of 25 paise per cm2 , to the nearest rupee.

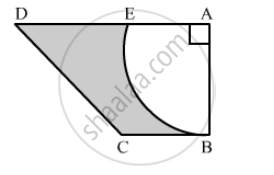
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
A circular park has a path of uniform width around it. The difference between the outer and inner circumferences of the circular path is 132 m. Its width is
The circumference of a circle is 100 m. The side of a square inscribed in the circle is
The perimeter of a certain sector of a circle of radius 6.5 cm in 31 cm. Find the area of the sector.
A roller has a diameter of 1.4 m. Find :
(i) its circumference ;
(ii) the number of revolutions it makes while travelling 61.6 m.
Is the area of the largest circle that can be drawn inside a rectangle of length a cm and breadth b cm (a > b) is πb2 cm2? Why?
