Advertisements
Advertisements
प्रश्न
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
उत्तर
Let the radii of two circles be r1 and r2 respectively.
Sum of the areas of two circles = 130π sq. cm
⇒ πr12 + πr22 = 130π
⇒ r12 + r22 = 130 ….(i)
Also, distance between two radii = 14 cm
⇒ r1 + r2 = 14
⇒ r1 = (14 - r2)
Substituting the value of r1 in (i), we get
(14 - r2)2 + r22 = 130
⇒ 196 - 28r2 + r22 + r22 = 130
⇒ 2r22 - 28r2 + 66 = 0
⇒ r22 - 14r2 + 33 = 0
⇒ r22 - 11r2 - 3r2 + 33 = 0
⇒ r2 (r2 - 11) - 3 (r2 - 11) = 0
⇒ (r2 - 11) (r2 - 3) = 0
⇒ r2 = 11 or r2 = 3
⇒ r1 = 14 - 11 = 3 or r1 = 14 - 3 = 11
Thus, the radii of two circles are 11 cm and 3 cm respectively.
APPEARS IN
संबंधित प्रश्न
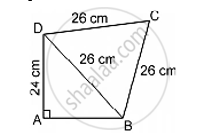
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
Find the area of a parallelogram with base equal to 25 cm and the corresponding height measuring 16.8 cm.
Find the area of a shaded region in the the following figure,where a circular arc of radius 7 cm has been drawn with vertex A of an equilateral triangle ABC of side 14 cm as centre. (Use π = 22/7 and \[\sqrt{3}\] = 1.73)
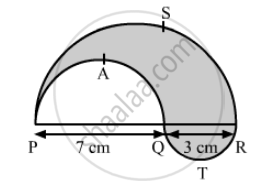
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
What is the angle subtended at the centre of a circle of radius 6 cm by an arc of length 3 π cm?
If the adjoining figure is a sector of a circle of radius 10.5 cm, what is the perimeter of the sector? (Take \[\pi = 22/7\])
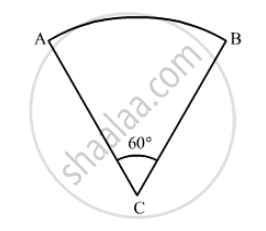
In the following figure, the shaded area is

The minute hand of a clock is 12 cm long. Find the area swept by in it 35 minutes.
A square tank has an area of 1600 cm2. There are four semicircular plots around it. Find the cost of turfing the plots at Rs 12.50 per m2
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed in kilometre per hour is the bicycle traveling?
