Advertisements
Advertisements
प्रश्न
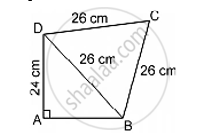
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
उत्तर
ΔBDC is an equilateral triangle with side `a=26` cm
Area of ΔBDC=` sqrt3/4 a^2`
=`sqrt3/4xx26^2`
=`1.73/4xx676`
=`292.37 cm^2`
By using Pythagoras theorem in the right – angled triangle `Δ DAB, `We get
` AD^2+AB^2=BD^2`
⇒` 24^2+AB^2=26^2`
⇒`AB^2=26^2-24^2`
⇒`AB^2=676-576`
⇒ `AB^2=100`
⇒`AB=10 cm`
Area of the `Δ ABD=1/2 xxbxxh`
=`1/2xx10xx24`
=`120 cm^2`
Area of the quadrilateral
= Area of the quadrilateral
= Are of ΔBCD+Area of ΔABD
=`292.37+120`
=`412.37 cm^2`
Perimeter of the quadrilateral
=AB+AC+CD+AD
= `24+10+26+26`
=86 cm
APPEARS IN
संबंधित प्रश्न
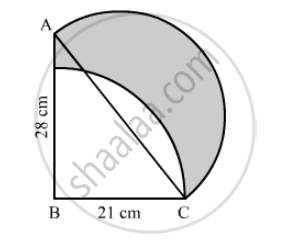
In the following figure, ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
What is the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal?
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
If the numerical value of the area of a circle is equal to the numerical value of its circumference , find its radius.
The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
In the following figure, the shaded area is

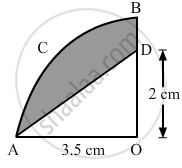
In the given figure, OABC is a quadrant of a circle of radius 3.5 cm with centre O. If OD = 2 cm, find the area of the shaded portion.
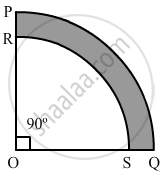
In the given figure, PQRS represents a flower bed. If OP = 21 m and OR = 14 m, find the area of the flower bed.
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
