Advertisements
Advertisements
प्रश्न
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
उत्तर

In this figure, centre of the circle is O, radius OA = r and ∠ AOB=θ
We are going to find the area of the segment AXB.
Area of the segment AXB=Area of the sector `OAXB-"Area of" ΔAOB`...........(1)
We know that area of the sector `OAXB=θ/360xxpi r^2`
We also know that area of `ΔAOB=r^2 sin θ/2 cos θ/2`
Substituting these values in equation (1) we get,
`"Area of the segment AXB"=θ/360 xxpi r^2-r^2 sin θ/2 cos θ/2`
`"Area of the segment AXB"=(θ/360 xxpi-sin θ/2 cos θ/2 )r^2`
`"So Area of the segment AXB"=((piθ)/360-sin θ/2 cos θ/2 )r^2`
Therefore, area of the segment is` ((piθ)/360-sin θ/2 cos θ/2) r^2`
APPEARS IN
संबंधित प्रश्न
A rectangular park 358 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it. Find the area to be laid with grass.
The cost of fencing a square lawn at ₹ 14 per meter is ₹ 28000. Find the cost of mowing the lawn at ₹ 54 100 per `m^2`
In the following figure, PQRS is a square of side 4 cm. Find the area of the shaded square.
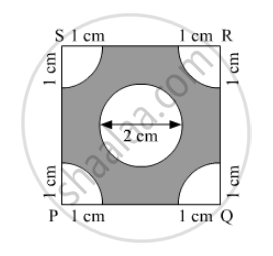
In the following figure, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.

In the following figure, AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.

What is the diameter of a circle whose area is equal to the sum of the areas of two circles of diameters 10 cm and 24 cm?
If three circles of radius a each, are drawn such that each touches the other two, prove that the area included between them is equal to `4/25"a"^2`.
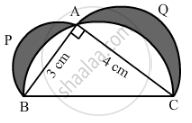
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
Find the area of the biggest circle that can be cut from a rectangular piece 44cm by 28cm. also, find the area of the paper left after cutting out the circle.
If radius of a circle is increased to twice its original length, how much will the area of the circle increase?
