Advertisements
Advertisements
प्रश्न
In the given figure, ∆ABC is right-angled at A. Semicircles are drawn on AB, AC and BC as diameters. It is given that AB = 3 cm and AC = 4 cm. Find the area of the shaded region.
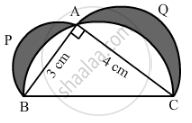
उत्तर
In triangle ΔABC, we have:
`BC = sqrt("AB"^2 + "AC"^2)`
`=sqrt(9+16)`
`=sqrt(25)`
= 5 cm
Ar(shaded part) = Ar(ΔABC) + Ar(semicircle APB) + Ar(semicircle AQC) - Ar(semicircle BAC)
`= (1/2xx3xx4)+(1/2pixx1.5xx1.5)+(1/2pixx2xx2)-(1/2pixx2.5xx2.5)`
`= {6 + 1/2pi(4+9/4-25/4)}`
= 6 + 0
= 6 cm2
APPEARS IN
संबंधित प्रश्न
The area of a rectangular plot is ` 462m^2` and is length is 28 m. Find its perimeter.
The floor of a rectangular hall is 24 m long and 18 m wide. How many carpets, each of length 2.5 m and breadth 80 cm, will be required to cover the floor of the hall?
In the following figure, the boundary of the shaded region consists of four semi-circular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, find
the length of the boundary.
the area of the shaded region.

The ratio of the outer and inner perimeters of a circular path is 23 : 22. If the path is 5 metres wide, the diameter of the inner circle is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then its radius is
If the area of a sector of a circle bounded by an arc of length 5π cm is equal to 20π cm2, then the radius of the circle
The length of the minute hand of a clock is 21 cm. The area swept by the minute hand in 10 minutes is
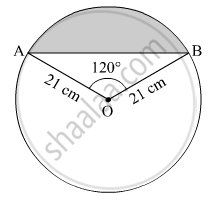
Find the area of the segment shown in Fig. 2, if the radius of the circle is 21 cm and ∠AOB = 120° `( "Use" π = (22)/(7))`
The floor of the circular swimming pool whose radius is 7 m has to be cemented at the rate of ₹ 18 per m2. Find the total cost of cementing the floor
If the radius of a circle is tripled, the area becomes ______.
