Advertisements
Advertisements
प्रश्न
PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semicircles are drawn with PQ and QS as diameters, as shown in the given figure. If PS = 12 cm, find the perimeter and area of the shaded region.
उत्तर
Perimeter (circumference of the circle) = 2πr
We know:
Perimeter of a semicircular arc = πr
Now,
For the arc PTS, radius is 6 cm.
∴ Circumference of the semicircle PTS =πr = 6π cm
For the arc QES, radius is 4 cm.
∴ Circumference of the semicircle QES = πr = 4π cm
For the arc PBQ, radius is 2 cm.
∴ Circumference of the semicircle PBQ = πr = 2π cm
Now,
Perimeter of the shaded region == 6π + 4π + 2π
= 12πcm
= 12 ×3.14
= 37.68 cm
Area of the semicircle PBQ `=1/2 pi"r"^2`
`= 1/2xx3..14xx2xx2`
= 6.28 cm2
Area of the semicircle PTS `= 1/2pi"r"^2`
`=1/2xx3.14xx6xx6`
= 56.52 cm2
Area of the semicircles QES `= 1/2pi"r"^2`
`=1/2xx3.14xx4xx4`
= 25.12 cm2
Area of the shaded region = Area of the semicircle PBQ + Area of the semicircle PTS - Area of the semicircle QES = 6.28 + 56.52 - 25.12 = 37.68 cm2
APPEARS IN
संबंधित प्रश्न
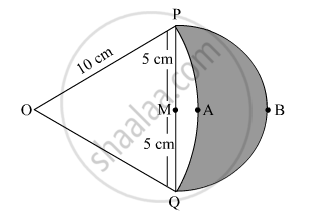
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
The inner circumference of a circular track is 220 m. The track is 7m wide everywhere. Calculate the cost of putting up a fence along the outer circle at the rate of j – 2 per metre. (Use π = 22/7)
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
Find the area of trapezium whose parallel sides are 11 m and 25 m long, and the nonparallel sides are 15 m and 13 m long.
The circumference of a circle is 22 cm. Find the area of its quadrant.
Find the radius of a circle whose perimeter and area are numerically equal.
In a circle of radius 10.5 cm, the minor arc is one-fifth of the major arc. Find the area of the sector corresponding to the major arc.
Find the diameter of the sphere for the following :
Volume = `72pi "cm"^3`
If the perimeter of a semi-circular protractor is 36 cm. Find its diameter.
The distance around a circle is its ______.
