Advertisements
Advertisements
प्रश्न
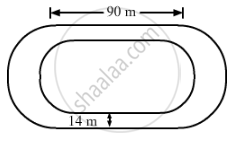
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
उत्तर
Length of the inner curved portion (400 - 2 × 90) = 220 m
∴ Length of each inner curved path`=220/2=110 "m"`
Thus, we have:
⇒ πr = 110
`⇒ 22/7"r" = 110`
`=> "r" = (110xx7)/22`
⇒ r =35m
Inner radius = 35 m
Outer radius = (35 + 14) = 49 m
Area of track = {Area of the two rectangles [each(90 × 14)] + Area of the circular ring with R = 49 m and r = 35 m)}
`=(2xx90xx14)+22/7xx[(49)^2-(35)^2]`
`=2520 + 22/7xx(2401-1225)`
`= 2520 + 22/7xx1176`
= 2520 + 3696
= 6216 m2
Length of the outer boundary of the track
`=(2xx90+2xx22/7xx49)`
= 488 m
Therefore, the length of the outer boundary of the track is 488 m and the area of the track is 6216 sq. m.
APPEARS IN
संबंधित प्रश्न
Below fig shows a sector of a circle, centre O. containing an angle 𝜃°. Prove that
Area of shaded region is`r^2/2(tantheta −(pitheta)/180)`
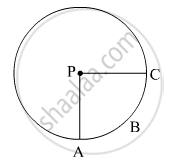
In the given figure, if A(P-ABC) = 154 cm2 radius of the circle is 14 cm, find
(1) `∠APC`
(2) l ( arc ABC) .
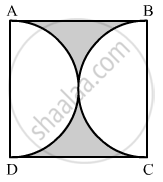
In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
The perimeter of a circular field is 242 m. The area of the field is
The radii of two concentric circles are 19 cm and 16 cm respectively. The area of the ring enclosed by these circles is
The area of a circular ring enclosed between two concentric circles is 88 cm 2. Find the radii of the two circles, if their difference is 1 cm.
The diameter of a right circular cylinder is 12 m and the slant height is 10 m. Find its curved surface area and the total surface area .
The speed of a car is 66km per hour. If each wheel of the car is 140cm in diameter, find the number if revolution made by each wheel per minute.
The circumference o a garden roller is 280cm. How many revolutions does it make in moving 490m?
In the formula, C = 2πr, ‘r’ refers to
