Advertisements
Advertisements
प्रश्न
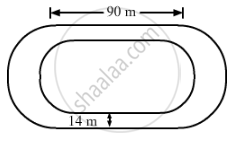
The inside perimeter of a running track shown in the figure is 400 m. The length of each of the straight portions is 90 m, and the ends are semicircles. If the track is 14 m wide everywhere, find the area of the track. Also, find the length of the outer boundary of the track.
उत्तर
Length of the inner curved portion (400 - 2 × 90) = 220 m
∴ Length of each inner curved path`=220/2=110 "m"`
Thus, we have:
⇒ πr = 110
`⇒ 22/7"r" = 110`
`=> "r" = (110xx7)/22`
⇒ r =35m
Inner radius = 35 m
Outer radius = (35 + 14) = 49 m
Area of track = {Area of the two rectangles [each(90 × 14)] + Area of the circular ring with R = 49 m and r = 35 m)}
`=(2xx90xx14)+22/7xx[(49)^2-(35)^2]`
`=2520 + 22/7xx(2401-1225)`
`= 2520 + 22/7xx1176`
= 2520 + 3696
= 6216 m2
Length of the outer boundary of the track
`=(2xx90+2xx22/7xx49)`
= 488 m
Therefore, the length of the outer boundary of the track is 488 m and the area of the track is 6216 sq. m.
APPEARS IN
संबंधित प्रश्न
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150º. Find the length of its arc and area.
Find the circumference of the circle with the following radius: (Take `bb(pi = 22/7`)
21 cm
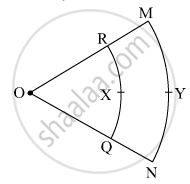
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
The wheel of a motor cycle is of radius 35 cm. How many revolutions per minute must the wheel make so as to keep a speed of 66 km/hr ?
A sector of 56°, cut out from a circle, contains 17.6 cm2. Find the radius of the circle.
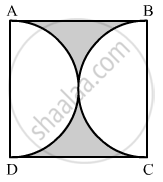
In the given figure, find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 8 cm , diameter = 12 cm
A wheel has a diameter of 84 cm. Find how many completer revolutions must it make to cover 3.168 km.
Circumferences of two circles are equal. Is it necessary that their areas be equal? Why?
A circle with radius 16 cm is cut into four equal parts and rearranged to form another shape as shown in the below figure:
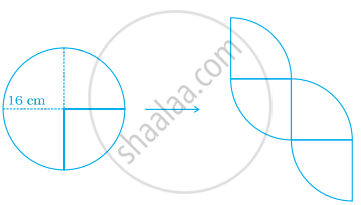
Does the perimeter change? If it does change, by how much does it increase or decrease?
