Advertisements
Advertisements
प्रश्न
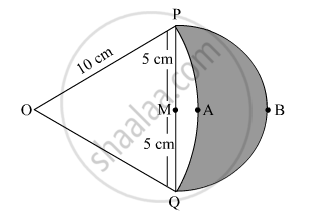
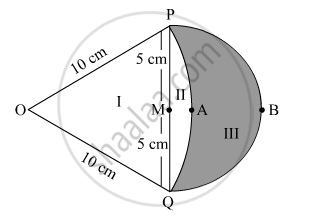
In Fig. 7, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre O and radius OP while arc PBQ is a semi-circle drawn on PQ ad diameter with centre M. If OP = PQ = 10 cm show that area of shaded region is `25(sqrt3-pi/6)cm^2`.
उत्तर
Given: OP = OQ = 10 cm
It is known that tangents drawn from an external point to a circle are equal in length.
So,
OP = OQ = 10 cm
Therefore, ∆ABC is an equilateral triangle.
⇒∠POQ=60°
Now
Area of part II = Area of the sector − Area of the equilateral triangle POQ
`=(/_POQ)/360^@xxpir^2-sqrt3/4xx(10)^2`
`=60^@/360^@xxpi(10^2)-sqrt3/4xx(10)^2`
`=100(pi/6-sqrt3/4) `
Area of the semicircle on diameter PQ = Area of part II + Area of part III
`1/2xxpi(5)^2=25/2pi`
∴ Area of the shaded region (part III)
`=25/2pi-100(pi/6-sqrt3/4)`
`=25/2pi-100/6pi+25sqrt3`
`=25sqrt3-25/6pi`
`=25(sqrt3-pi/6)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
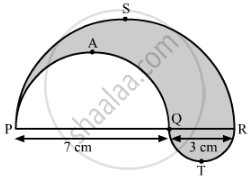
In PSR, RTQ and PAQ are three semicircles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of the shaded region. [Use π=3.14]
Find the area of circle whose circumference is 44 cm.
Four equal circles each of radius a, touch each other. Show that area between them is `6/7a^2`
Find the area of the rhombus, the length of whose diagonals are 30 cm and 16 cm. Also, find the perimeter of the rhombus.
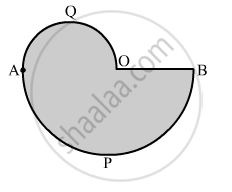
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
A bucket is raised from a well by means of a rope wound round a wheel of diameter 35 cm. If the bucket ascends in 2 minutes with a uniform speed of 1.1 m per sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
Find the area and perimeter of the following sector :
Diameter = 42 cm, angle at the centre is 100·.
The diameters of the front and the rear wheels of a tractor are 63 cm and 1.54 m respectively. The rear wheel is rotating at `24 6/11` revolutions per minute. Find:
(i) the revolutions per minute made by the front wheel.
(ii) the distance traveled bu the tractor in 40 minutes.
The radius of a circle is 21 cm. Find the circumference (Take π = `3 1/7`).
The wheel of a bullock cart has a diameter of 1.4 m. How many rotations will the wheel complete as the cart travels 1.1 km?
