Advertisements
Advertisements
प्रश्न
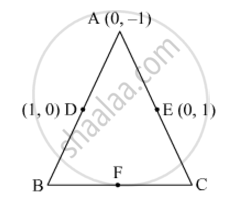
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
उत्तर
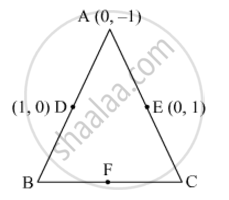
Let the coordinates of B and C be (x2, y2) and (x3, y3), respectively.
D is the midpoint of AB.
So,
`(1,0)=((x_2+0)/2,(y_2-1)/2)`
`=>1 = x_2/2 `
⇒ x2 = 2 and y2 = 1
Thus, the coordinates of B are (2, 1).
Similarly, E is the midpoint of AC.
So,
`(0,1)=((x_3+0)/2, (y_3-1)/2)`
`=>0=x_3/2 `
⇒ x3 = 0 and y3 = 3
Thus, the coordinates of C are (0, 3).
Also, F is the midpoint of BC. So, its coordinates are
`((2+0)/2,(1+3)/2)=(1,2)`
Now,
Area of a triangle = `1/2`[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
Thus, the area of ∆ABC is
`1/2[0(1-3)+2(3+1)+0(-1-1)]`
`=1/2xx8`
=4 square units
And the area of ∆DEF is
`1/2`[1(1−2)+0(2−0)+1(0−1)]
`=1/2xx(-2)`
=1 square unit (Taking the numerical value, as the area cannot be negative)
APPEARS IN
संबंधित प्रश्न
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
If D, E and F are the mid-points of sides BC, CA and AB respectively of a ∆ABC, then using coordinate geometry prove that Area of ∆DEF = `\frac { 1 }{ 4 } "(Area of ∆ABC)"`
Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
The four vertices of a quadrilateral are (1, 2), (−5, 6), (7, −4) and (k, −2) taken in order. If the area of the quadrilateral is zero, find the value of k.
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
Find the missing value:
| Base | Height | Area of Triangle |
| ______ | 31.4 mm | 1256 mm2 |
