Advertisements
Advertisements
प्रश्न
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
उत्तर
We have to find the co-ordinates of the third vertex of the given triangle. Let the co-ordinates of the third vertex be(x,y).
The co-ordinates of other two vertices are (1, 2) and (3, 5)
The co-ordinate of the centroid is (0, 0)
We know that the co-ordinates of the centroid of a triangle whose vertices are
`(x_1,y_1),(x_2,y_2),(x_3,y_3)`is
`((x_1+x_2+x_3)/3,(y_1+y_2+y_3)/3)`
So,
`(0,0)=((x+1+3)/3,(y+2+5)/3) or ((4+x)/3,(7+y)/3)`
Compare individual terms on both the sides -
`(4+x)/3 = 0
⇒ 4 + x = 0
⇒ x = -4
and
`(7+y)/3=0`
⇒ 7 + y = 0
⇒ y = -7
So the co-ordinate of third vertex (-4, -7)
APPEARS IN
संबंधित प्रश्न
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and (5k – 1, 5k) are collinear.
The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the following figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of Δ PQR if C is the origin?
Also calculate the areas of the triangles in these cases. What do you observe?
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
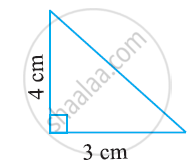
Find the area of the following triangle:
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
Find the area of ΔABC whose vertices are:
A( 3,8) , B(-4,2) and C( 5, -1)
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
