Advertisements
Advertisements
Question
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
Solution
We have to find the co-ordinates of the third vertex of the given triangle. Let the co-ordinates of the third vertex be(x,y).
The co-ordinates of other two vertices are (1, 2) and (3, 5)
The co-ordinate of the centroid is (0, 0)
We know that the co-ordinates of the centroid of a triangle whose vertices are
`(x_1,y_1),(x_2,y_2),(x_3,y_3)`is
`((x_1+x_2+x_3)/3,(y_1+y_2+y_3)/3)`
So,
`(0,0)=((x+1+3)/3,(y+2+5)/3) or ((4+x)/3,(7+y)/3)`
Compare individual terms on both the sides -
`(4+x)/3 = 0
⇒ 4 + x = 0
⇒ x = -4
and
`(7+y)/3=0`
⇒ 7 + y = 0
⇒ y = -7
So the co-ordinate of third vertex (-4, -7)
APPEARS IN
RELATED QUESTIONS
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
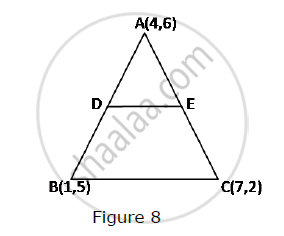
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
For what values of k are the points A(8, 1) B(3, -2k) and C(k, -5) collinear.
A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of ₹ 45 per sq.m2
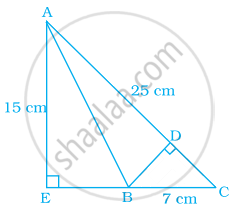
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.