Question

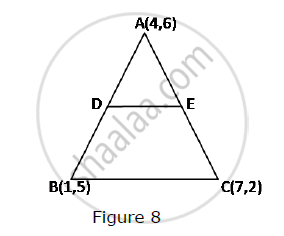
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.

Answer 1

`(AD)/(AB)=(AE)/(AC)=1/3`

`:.(AB)/(AD)=(AC)/(AE)=3`

`:.(AD+DB)/(AD)=(AE+EC)/(AE)=3`

`:.1+(DB)/(AD)=1+(EC)/(AE)=3`

`:.(DB)/(AD)=(EC)/(AE)=2`

`:.(AD)/(DB)=(AE)/(EC)=1/2`

∴ AD:DB = AE :EC = 1: 2

So, D and E divide AB and AC respectively in the ratio 1:2.

So the coordinates of D and E are

`((1+8)/(1+2),(5+12)/(1+2))=(3,17/3) `

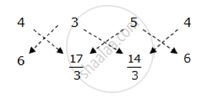
Area of ΔADE

`=1/2|(4xx17/3+3xx14/3+5xx6)-(3xx6+5xx17/3+4xx14/3)|`

`=1/2|(68/3+14+30)-(18+85/3+56/3)|`

`=1/2|((68+42+90)/3)-((54+85+56)/3)|`

`=1/2|(200/3)-(195/3)|`

`=1/2xx5/3`

`=5/6 `

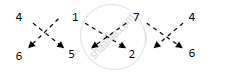
Area of ΔABC

`=1/2|(4xx5+1xx2+7xx6)-(1xx6+7xx5+4xx2)|`

`=1/2|(20+2+42)-(6+35+8)|`

`=1/2|64-49|`

`=15/2`

`:.(`