Advertisements
Advertisements
Question
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
Solution 1
The Vertices of ΔABC are A (2, 3), B (3, 5), and C (4, 4)
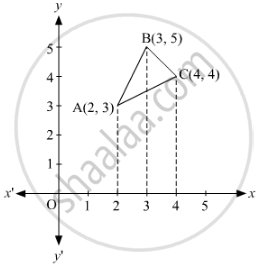
Equation of line segment AB is
`("y" - 5) = (5-3)/(3-2) ("x" -3)`
=`"y" -5 = 2 ("x" -3)`
=`"y" = 2"x" -1`
Equation of line segment BC is
`("y" - 5) = (5-3)/(3-4) ("x" -3)`
=`"y" -5 = -1 ("x" -3)`
=`"y" = -"x" + 8`
Equation of line segment AC is
`("y" - 4) = (4-3)/(4-2) ("x" -4)`
=`"y" -4 = (1)/(2) ("x" -4)`
= `"y" = ("x")/(2) + 2`
∴ Area of ΔABC = `int_2^3 [(2"x" -1) - ("x"/2+2)] d"x" + int_3^4 [(-"x" + 8) - ("x"/2 + 2)] . d"x"`
= `int_2^3 ((3"x")/2 -3) . d"x" + int_3^4 ((-3"x")/2 + 6) . d"x"`
= `[(3"x"^2)/(4) - 3"x"]_2^3 + [ (-3"x"^2)/4 + 6"x"]_3^4`
= `(27/4 - 9) - (3 -6) + (-12 + 24) - (-27/4 + 18)`
= `(3)/(2) "sq. units"`.
Solution 2
The Vertices of ΔABC are A (2, 3), B (3, 5), and C (4, 4)
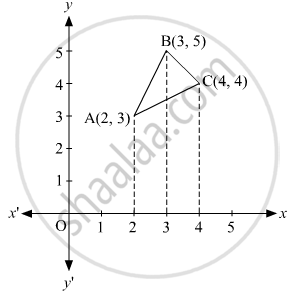
Equation of line segment AB is
`("y" - 5) = (5-3)/(3-2) ("x" -3)`
=`"y" -5 = 2 ("x" -3)`
=`"y" = 2"x" -1`
Equation of line segment BC is
`("y" - 5) = (5-3)/(3-4) ("x" -3)`
=`"y" -5 = -1 ("x" -3)`
=`"y" = -"x" + 8`
Equation of line segment AC is
`("y" - 4) = (4-3)/(4-2) ("x" -4)`
=`"y" -4 = (1)/(2) ("x" -4)`
= `"y" = ("x")/(2) + 2`
∴ Area of ΔABC = `int_2^3 [(2"x" -1) - ("x"/2+2)] d"x" + int_3^4 [(-"x" + 8) - ("x"/2 + 2)] . d"x"`
= `int_2^3 ((3"x")/2 -3) . d"x" + int_3^4 ((-3"x")/2 + 6) . d"x"`
= `[(3"x"^2)/(4) - 3"x"]_2^3 + [ (-3"x"^2)/4 + 6"x"]_3^4`
= `(27/4 - 9) - (3 -6) + (-12 + 24) - (-27/4 + 18)`
= `(3)/(2) "sq. units"`.
APPEARS IN
RELATED QUESTIONS
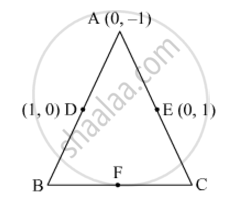
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
Find the area of the quadrilateral ABCD whose vertices are respectively A(1, 1), B(7, –3), C(12, 2) and D(7, 21).
For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
The two opposite vertices of a square are (− 1, 2) and (3, 2). Find the coordinates of the other two vertices.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
Find the area of the following triangle:

If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Find the area of ΔABC whose vertices are:
A(-5,7) , B (-4,-5) and C (4,5)
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:
Using determinants, find the values of k, if the area of triangle with vertices (–2, 0), (0, 4) and (0, k) is 4 square units.
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of ₹ 45 per sq.m2
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
Find the area of the triangle whose vertices are (-2, 6), (3, -6), and (1, 5).
Let `Delta = abs (("x", "y", "z"),("x"^2, "y"^2, "z"^2),("x"^3, "y"^3, "z"^3)),` then the value of `Delta` is ____________.
Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs 7 per m2.
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is ______.

Area of a triangle = `1/2` base × ______.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
