Advertisements
Advertisements
Question
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
Solution
| Base | Height | Area of Triangle |
| 22 cm | 15.5 | 170.5 cm2 |
Explanation:
b = 22 cm
h = ?
Area = `1/2 xx b xx h` = 170.5 cm2
`1/2 xx 22 xx h` = 170.5 cm2
h = `(170.5 xx 2)/22`
h = 15.5 cm
Therefore, the height of such triangle is 15.5 cm.
RELATED QUESTIONS
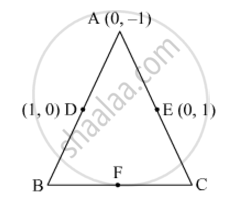
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
Find the third vertex of a ΔABC if two of its vertices are B(-3,1) and C (0,-2) and its centroid is at the origin
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Prove that the points A (a,0), B( 0,b) and C (1,1) are collinear, if `( 1/a+1/b) =1`.
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?
Find the area of the following triangle:

If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
The area of a triangle with vertices A, B, C is given by ______.
