Advertisements
Advertisements
Question
Find the third vertex of a ΔABC if two of its vertices are B(-3,1) and C (0,-2) and its centroid is at the origin
Solution
Two vertices of ΔABC are B(-3,1) and C (0,-2) .Let the third vertex be A (a, b). Then, the coordinates of its centroid are
`((-3+0+a)/3, (1-2+b)/3)`
i.e `((-3+a)/3 , (-1+b)/3)`
But it is given that the centroid is at the origin, that is G (0,0) Therefore
`0= ((-3+a)/3,0=(-1+b)/3)`
⇒ 0=-3+a,0=-1+b
⇒3= a,1=b
⇒ a=3, b=1
Therefore, the third vertex of ΔABC A(3,1).
APPEARS IN
RELATED QUESTIONS
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10
The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4), then k is ______.
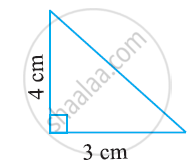
Find the area of the following triangle:
prove that the points A (7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
Find the values of k if the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
