Advertisements
Advertisements
Question
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
Solution
The area of a triangle with vertices (x1, y1), (x2, y2) and (x3, y3) is given by
Δ = `1/2 |(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|`
Also, area of an equilateral triangle with side a is given by
Δ = `sqrt(3)/2 "a"^2`
∴ `1/2 |(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)| = sqrt(3)/4 "a"^2`
Squaring both sides, we get
⇒ Δ2 = `1/4 |(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)| = 3/16 "a"^4`
or `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
APPEARS IN
RELATED QUESTIONS
Find the values of k so that the area of the triangle with vertices (k + 1, 1), (4, -3) and (7, -k) is 6 sq. units.
The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Find the area of a triangle with vertices at the point given in the following:
(2, 7), (1, 1), (10, 8)
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Find values of k if area of triangle is 4 square units and vertices are (k, 0), (4, 0), (0, 2)
Find the area of the following triangle:

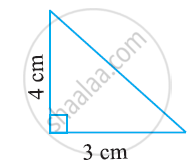
Find the area of the following triangle:
ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
If G(-2, 1) is the centroid of a ΔABC and two of its vertices are A(1, -6) and B(-5, 2) , find the third vertex of the triangle.
Find the area of ΔABC whose vertices are:
A( 3,8) , B(-4,2) and C( 5, -1)
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
If `D((-1)/2, 5/2), E(7, 3)` and `F(7/2, 7/2)` are the midpoints of sides of ∆ABC, find the area of the ∆ABC.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
