Advertisements
Advertisements
Question
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Solution
The vertices of the triangle are A(7, -3), B(5,3) and C(3,-1)
`"Coordinates of" D = ((5+3)/2,(3-1)/2) = (4,1)`
For the area of the triangle ADC, let
`A (x_1,y_1)=A(7,-3), D(x_2,y_2) =D(4,1) and C (x_3,y_3) = C(3,-1)`. Then
`"Area of" Δ ADC = 1/2 [ x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`=1/2 [7(1+1)+4(-1+3)+3(-3-1)]`
`=1/2[14+8-12}=5` sq. unit
Now, for the area of triangle ABD, let
`A(x_1,y_1) = A(7,-3), B(x_2,y_2) = B(5,3) and D (x_3,y_3) = D (4,1). `Then
`"Area of" Δ ADC = 1/2 [ x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`=1/2 [7(3-1)+5(1+3)+4(-3-3)]`
`=1/2[14+20-24] = 5` sq. unit
Thus, Area (ΔADC) = Area (ΔABD) = 5. sq units
Hence, AD divides ΔABC into two triangles of equal areas.
APPEARS IN
RELATED QUESTIONS
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is
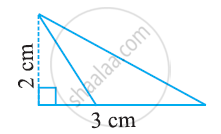
Find the area of the following triangle:
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

In the given figure, if PR = 12 cm, QR = 6 cm and PL = 8 cm, then QM is ______.

If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
