Advertisements
Advertisements
प्रश्न
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
उत्तर
The vertices of the triangle are A(7, -3), B(5,3) and C(3,-1)
`"Coordinates of" D = ((5+3)/2,(3-1)/2) = (4,1)`
For the area of the triangle ADC, let
`A (x_1,y_1)=A(7,-3), D(x_2,y_2) =D(4,1) and C (x_3,y_3) = C(3,-1)`. Then
`"Area of" Δ ADC = 1/2 [ x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`=1/2 [7(1+1)+4(-1+3)+3(-3-1)]`
`=1/2[14+8-12}=5` sq. unit
Now, for the area of triangle ABD, let
`A(x_1,y_1) = A(7,-3), B(x_2,y_2) = B(5,3) and D (x_3,y_3) = D (4,1). `Then
`"Area of" Δ ADC = 1/2 [ x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
`=1/2 [7(3-1)+5(1+3)+4(-3-3)]`
`=1/2[14+20-24] = 5` sq. unit
Thus, Area (ΔADC) = Area (ΔABD) = 5. sq units
Hence, AD divides ΔABC into two triangles of equal areas.
APPEARS IN
संबंधित प्रश्न
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and (5k – 1, 5k) are collinear.
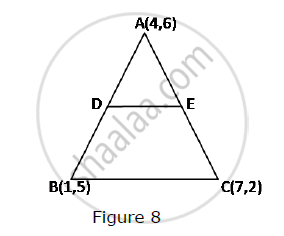
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4), then k is ______.
Prove that the points A (a,0), B( 0,b) and C (1,1) are collinear, if `( 1/a+1/b) =1`.
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
If the points (a1, b1), (a2, b2) and(a1 + a2, b1 + b2) are collinear, then ____________.
Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
