Advertisements
Advertisements
Question
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

Solution
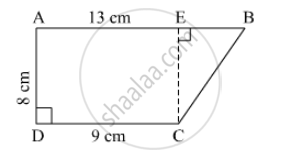
Draw perpendicular from C to line AB. Name the point E.
CE = AD = 8 cm
EB = AB − AE = AB − CD = 13 − 9 = 4cm
∴ Area of of a trapezium = `1/2 xx "sum of lengths of parallel sides" xx h`
A (☐ABCD) = `1/2 xx [l(AB) + l(DC)] xx l(AD)`
= `1/2 xx (13 + 9) xx 8`
= `1/2 xx 22 xx 8`
= 11 x 8
= 88 sq. cm
∴ The area of ☐ABCD is 88 sq. cm.
RELATED QUESTIONS
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 15 cm | 154.5 cm2 |
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

