Advertisements
Advertisements
Question
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
Solution
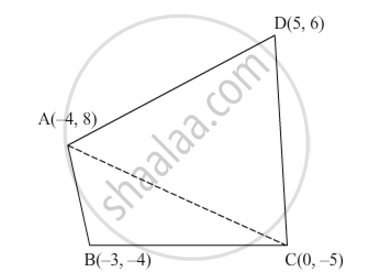
Let the vertices of the quadrilateral be A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6).
Join AC to form two triangles, namely, ΔABC and ΔACD.
Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD
We know
Area of triangle having vertices (x1, y1), (x2, y2) and (x3, y3) =`1/2`[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
Now,
Area of ∆ABC=`1/2`{(−4)[(−4)−(−5)]+(−3)[(−5)−(8)]+(0)[(8)−(−4)]}
=`1/2`(−4+39)
`=35/2 `
Area of ∆ACD=`1/2`{(−4)[(−5)−(6)]+(0)[(6)−(8)]+(5)[(8)−(−5)]}
=`1/2`(44+65)
`=109/2`
∴Area of quadrilateral ABCD=Area of ∆ABC+Area of ∆ACD
`35/2+109/2`
=72 square units
Thus, the area of quadrilateral ABCD is 72 square units.
RELATED QUESTIONS
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
For what values of k are the points A(8, 1) B(3, -2k) and C(k, -5) collinear.
Triangles having the same base have equal area.
In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

