Advertisements
Advertisements
Question
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
Solution
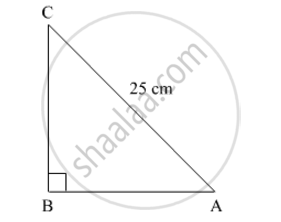
Let ABC be a right-angled triangle.
Since the perimeter of the right triangle is 60 cm,
AB + BC +CA = 60 cm
⇒ AB + BC + 25 = 60
⇒ AB + BC = 35 cm .....(1)
In ∆ABC,
AB2 + BC2 = CA2
⇒ (AB + BC)2 − 2(AB)(BC) = (25)2
⇒ (35)2 − 2(AB)(BC) = (25)2 [From (1)]
⇒ (35 − 25)(35 + 25) = 2(AB)(BC)'
⇒ (AB)(BC) = 300
Now,
Area of ∆ABC= `1/2`×AB×BC=`1/2`×300=150 cm2
Hence, the area of the triangle is 150 cm2.
APPEARS IN
RELATED QUESTIONS
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

Find the area of ΔABC whose vertices are:
A(-5,7) , B (-4,-5) and C (4,5)
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
The points (1,1), (-2, 7) and (3, -3) are ______.
The points (0, 5), (0, –9) and (3, 6) are collinear.
Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
