Advertisements
Advertisements
प्रश्न
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
उत्तर
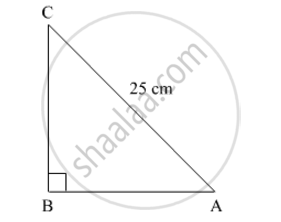
Let ABC be a right-angled triangle.
Since the perimeter of the right triangle is 60 cm,
AB + BC +CA = 60 cm
⇒ AB + BC + 25 = 60
⇒ AB + BC = 35 cm .....(1)
In ∆ABC,
AB2 + BC2 = CA2
⇒ (AB + BC)2 − 2(AB)(BC) = (25)2
⇒ (35)2 − 2(AB)(BC) = (25)2 [From (1)]
⇒ (35 − 25)(35 + 25) = 2(AB)(BC)'
⇒ (AB)(BC) = 300
Now,
Area of ∆ABC= `1/2`×AB×BC=`1/2`×300=150 cm2
Hence, the area of the triangle is 150 cm2.
APPEARS IN
संबंधित प्रश्न
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
Show that the following sets of points are collinear.
(2, 5), (4, 6) and (8, 8)
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq.units. The value of k will be ______.
Triangles having the same base have equal area.
