Advertisements
Advertisements
प्रश्न
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
उत्तर
Given, the pointsA(x,y), B(-5,7) and C(-4,5) are collinear.
So, the area formed by these vertices is 0.
1/2[x(7-5)+(-5)(5-y)+(-4)(y-7)= 0
1/2[2x-25+5y-4y+28]= 0
1/2[2x+y+3]= 0
2x+y+3 = 0
y = -2x- 3
APPEARS IN
संबंधित प्रश्न
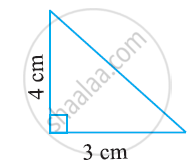
Find the area of the following triangle:
Find the area of the quadrilaterals, the coordinates of whose vertices are
(−3, 2), (5, 4), (7, −6) and (−5, −4)
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 15 cm | 154.5 cm2 |
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
