Advertisements
Advertisements
प्रश्न
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
उत्तर
Let us consider a Cartesian plane having a parallelogram OABC in which O is the origin.
We have to prove that middle point of the opposite sides of a quadrilateral and the join of the mid-points of its diagonals meet in a point and bisect each other.
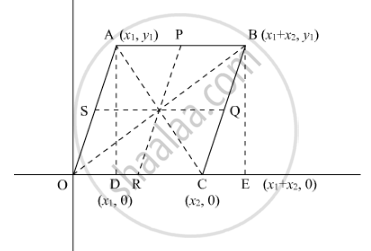
Let the co-ordinate of A be `(x_1,y_1)`. So the coordinates of other vertices of the quadrilateral are- O (0, 0); B`(x_1+x_2,y_1)`; C`(x_2,0)`
Let P, Q, R and S be the mid-points of the sides AB, BC, CD, DA respectively.
In general to find the mid-point p(x,y) of two points`A(x_1,y_-1)`and B`(x_2,y_2)` we use section formula as,
`P(x,y)=((x_1+x_2)/2,(y_1+y_2)/2)`
So co-ordinate of point P,
`=((x_1+x_2+x_1)/2,(y_1+y_-2)/2)`
`=((2x_1+x_1)/2,y_1/2)`
Similarly co-ordinate of point R,
`=(x_2/2,0)`
Similary co-ordinate of point S,
`=(x_1/2,y_1/2)`
Let us find the co-ordinates of mid-point of as,
`(((2x_1+x_2)/2+x_2/2)/2,y_1/2)`
`=((x_1+x_2)/ 2,y_1/2)`
Similarly co-ordinates of mid-point of Qs,
`=((x_1+x_2)/2,y_1/2)`
NOw the mid-pont of diagonal AC,
`=((x_1+x_2)/2,y_1/2)`
Similarly the mid-point of diagonal OA,
`((x_1+x_2)/2,y_1/2)`
Hence the mid-points of PR, QS, AC and OA coincide.
Thus, middle point of the opposite sides of a quadrilateral and the join of the mid-points of its diagonals meet in a point and bisect each other.
APPEARS IN
संबंधित प्रश्न
The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the following figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of Δ PQR if C is the origin?
Also calculate the areas of the triangles in these cases. What do you observe?
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, —3) and (3, 4), find the vertices of the triangle.
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
Find the area of ΔABC with A(1, -4) and midpoints of sides through A being (2, -1) and (0, -1).
Prove that the points A (a,0), B( 0,b) and C (1,1) are collinear, if `( 1/a+1/b) =1`.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
Ratio of areas of ∆MNO, ∆MOP and ∆MPQ in the given figure is ______.

