Advertisements
Advertisements
प्रश्न
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
उत्तर
Let us consider a Cartesian plane having a parallelogram OABC in which O is the origin.
We have to prove that middle point of the opposite sides of a quadrilateral and the join of the mid-points of its diagonals meet in a point and bisect each other.
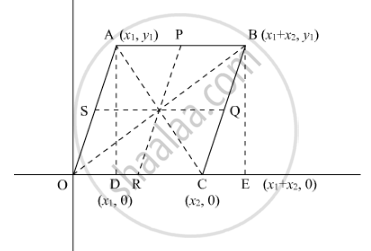
Let the co-ordinate of A be `(x_1,y_1)`. So the coordinates of other vertices of the quadrilateral are- O (0, 0); B`(x_1+x_2,y_1)`; C`(x_2,0)`
Let P, Q, R and S be the mid-points of the sides AB, BC, CD, DA respectively.
In general to find the mid-point p(x,y) of two points`A(x_1,y_-1)`and B`(x_2,y_2)` we use section formula as,
`P(x,y)=((x_1+x_2)/2,(y_1+y_2)/2)`
So co-ordinate of point P,
`=((x_1+x_2+x_1)/2,(y_1+y_-2)/2)`
`=((2x_1+x_1)/2,y_1/2)`
Similarly co-ordinate of point R,
`=(x_2/2,0)`
Similary co-ordinate of point S,
`=(x_1/2,y_1/2)`
Let us find the co-ordinates of mid-point of as,
`(((2x_1+x_2)/2+x_2/2)/2,y_1/2)`
`=((x_1+x_2)/ 2,y_1/2)`
Similarly co-ordinates of mid-point of Qs,
`=((x_1+x_2)/2,y_1/2)`
NOw the mid-pont of diagonal AC,
`=((x_1+x_2)/2,y_1/2)`
Similarly the mid-point of diagonal OA,
`((x_1+x_2)/2,y_1/2)`
Hence the mid-points of PR, QS, AC and OA coincide.
Thus, middle point of the opposite sides of a quadrilateral and the join of the mid-points of its diagonals meet in a point and bisect each other.
APPEARS IN
संबंधित प्रश्न
If P(–5, –3), Q(–4, –6), R(2, –3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
Prove that the points (2,3), (-4, -6) and (1, 3/2) do not form a triangle.
Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).
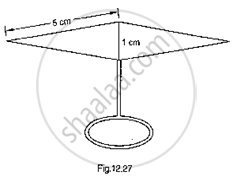
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
If the centroid of ΔABC having vertices A (a,b) , B (b,c) and C (c,a) is the origin, then find the value of (a+b+c).

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm. 
Find:
(i) the area of the ∆PQR
(ii) QM.
The points (0, 5), (0, –9) and (3, 6) are collinear.
