Advertisements
Advertisements
प्रश्न
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
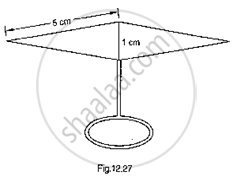
उत्तर
Area of the blades of magnetic compass = Area of ΔADB + Area of ΔCDB
Now, for area of ΔADB
Let, 2s = AD + DB + BA (Perimeter of ΔADB)
Semi perimeter (S)= `1/2(5+1+5)=11/2 cm`
By using heron’s formulae
Now, area of ΔADB `=sqrt(s(s-ad)(s-bd)(s-ba))`
`sqrt(11/2(11/2-5)(11/2-1)(11/2-5))`
`=2.49 cm^2`
= Also, area of triangle ADB = 𝐴𝑟𝑒𝑎 𝑜𝑓 Δ𝑙𝑒 𝐶𝐷𝐵
∴ Area of the blades of magnetic compass
= 2×(𝑎𝑟𝑒𝑎 𝑜𝑓 Δ𝐴𝐷𝐵)
= 2 × 2.49
= `4.98 m^2`
APPEARS IN
संबंधित प्रश्न
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
Find the area of ΔABC whose vertices are:
A(-5,7) , B (-4,-5) and C (4,5)
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
Show that ∆ ABC with vertices A (–2, 0), B (0, 2) and C (2, 0) is similar to ∆ DEF with vertices D (–4, 0), F (4, 0) and E (0, 4) ?
If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
