Advertisements
Advertisements
प्रश्न
If P(–5, –3), Q(–4, –6), R(2, –3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
उत्तर

The vertices of the quadrilateral PQRS are P(−5, −3), Q(−4, −6), R(2, −3) and S(1, 2).
Join QS to form two triangles, namely, ΔPQS and ΔRSQ.
Area of quadrilateral PQRS = Area of ΔPQS + Area of ΔRSQ
We know
Area of triangle having vertices (x1, y1), (x2, y2) and (x3, y3) = `1/2`[x1(y2−y3)+x2(y3−y1)+x3(y1−y2)]
Now,
Area of △PQS = `1/2`[−5(−6−2)+(−4)(2+3)+1(−3+6)]
=`1/2`[−5(−8)+(−4)(5)+1(3)]
=`1/2`(40−20+3)
=`23/2`square units
Area of ∆RSQ= `1/2`[2(2+6)+1(−6+3)+(−4)(−3−2)]
=`1/2`[2(8)+1(−3)+(−4)(−5)]
=`1/2`(16−3+20)
=`33/2` square units
Area of quadrilateral PQRS = Area of ΔPQS + Area of ΔRSQ
`=23/2+33/2`
`=56/2`
=28 square units
Thus, the area of quadrilateral PQRS is 28 square units.
संबंधित प्रश्न
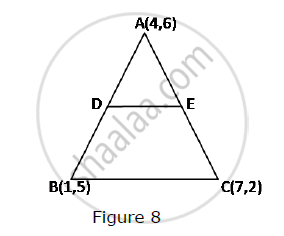
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Show that the following points are collinear:
A(8,1), B(3, -4) and C(2, -5)
Show that ∆ ABC with vertices A (–2, 0), B (0, 2) and C (2, 0) is similar to ∆ DEF with vertices D (–4, 0), F (4, 0) and E (0, 4) ?
A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of ₹ 45 per sq.m2
A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ∆ADE.
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
If area of a triangular piece of cardboard is 90 cm2, then the length of altitude corresponding to 20 cm long base is ______ cm.
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

