Advertisements
Advertisements
प्रश्न
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
विकल्प
14 cm
13 cm
12 cm
11 cm
उत्तर
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is 13 cm.
Explanation:
Given, area of a right-angled triangle = 30 cm2
and smallest side i.e. base = 5 cm
We know that,
Area of right angled triangle = `1/2` × Base × Height
∴ 30 = `1/2` × 5 × Height
⇒ Height = `(30 xx 2)/5`
⇒ Height = 12 cm
Now, according to Pythagoras theorem,
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ (Hypotenuse)2 = (12)2 + (5)2 ......[∵ Height = Percendicular]
⇒ (Hypotenuse)2 = 144 + 25
⇒ (Hypotenuse)2 = 169
⇒ Hypotenuse = `sqrt(169)`
⇒ Hypotenuse = 13 cm
APPEARS IN
संबंधित प्रश्न
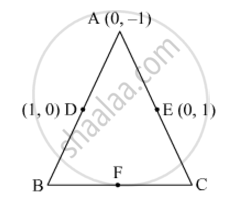
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
If the points A(−1, −4), B(b, c) and C(5, −1) are collinear and 2b + c = 4, find the values of b and c.
Find equation of line joining (3, 1) and (9, 3) using determinant.
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
A field is in the shape of a right angled triangle whose base is 25 m and height 20 m. Find the cost of levelling the field at the rate of ₹ 45 per sq.m2
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
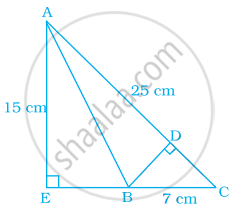
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.