Advertisements
Advertisements
प्रश्न
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
उत्तर
Let ABCD is a rectangular plot having a measurement of 40 m long and 15 m front.
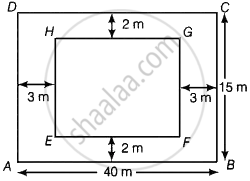
∴ Length of inner-rectangle, EF = 40 – 3 – 3 = 34 m
And breadth of inner-rectangle, FG = 15 – 2 – 2 = 11 m
∴ Another rectangle EFGH will be formed inside the rectangle ABCD
∴ Area of inner-rectangle, EFGH = Length × Breadth
= EF × FG ...[∴ Area of a rectangle = length × breadth]
= 34 × 11
= 374 m2
Hence, the largest area where the house can be constructed in 374 m2.
APPEARS IN
संबंधित प्रश्न
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
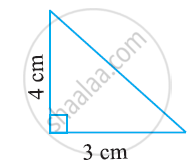
Find the area of the following triangle:
Prove that the points (2,3), (-4, -6) and (1, 3/2) do not form a triangle.
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
Ratio of areas of ∆MNO, ∆MOP and ∆MPQ in the given figure is ______.

Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
