Advertisements
Advertisements
प्रश्न
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
विकल्प
(a + b + c)2
0
a + b + c
abc
उत्तर
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is 0.
Explanation:
Let the vertices of a triangle are, A ≡ (x1, y1) ≡ (a, b + c)
B ≡ (x2, y2) ≡ (b, c + a) and C = (x3, y3) ≡ (c, a + b)
∵ Area of ΔABC = Δ = `1/2[x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)]`
∴ Δ = `1/2[a(c + a - a - b) + b(a + b - b - c) + c(b + c - c - a)]`
= `1/2[a(c - b) + b(a - c) + c(b - a)]`
= `1/2(ac - ab + ab - bc + bc - ac)`
= `1/2(0)`
= 0
Hence, the required area of triangle is 0.
APPEARS IN
संबंधित प्रश्न
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
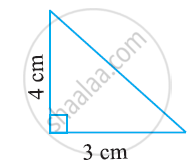
Find the area of the following triangle:
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Show that the points are the vertices of an isosceles right triangle.
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 5 feet | ? | 20 sq.feet |
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
