Advertisements
Advertisements
प्रश्न
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
उत्तर
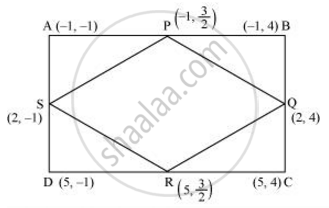
P is the mid point of side AB
THerefore the coordinates of P are ((-1-1)/2,(-1+4)/2) = (-1, 3/2)
Similary the coordinates of Q , R and S are (2,4),(5, 3/2), and (2, -1) respectilvely
Length of PQ =`sqrt((-1-2)^2 + (3/2-4)^2) =sqrt(9+25/4)= sqrt(61/4)`
Length of QR =`sqrt((2-5)^2 + (4-3/2)^2) =sqrt(9+25/4)= sqrt(61/4)`
Length of RS =`sqrt((5-2)^2 + (3/2+1)^2) =sqrt(9+25/4)= sqrt(61/4)`
Length of SP =`sqrt((2+1)^2 + (-1-3/2)^2) =sqrt(9+25/4)= sqrt(61/4)`
Length of PR =`sqrt((-1-5)^2 + (3/2-3/2)^2) = 6`
Length of QS = `sqrt((2-2)^2 + (4+1)^2) = 5`
It can be observed that all sides of the given quadrilateral are of the same measure. However, the diagonals are of different lengths. Therefore, PQRS is a rhombus.
APPEARS IN
संबंधित प्रश्न
If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
Find equation of line joining (1, 2) and (3, 6) using the determinant.
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle ?
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
