Advertisements
Advertisements
प्रश्न
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
उत्तर
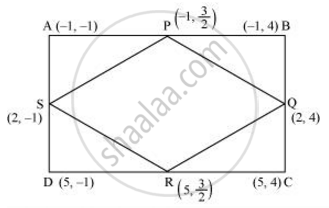
P is the mid point of side AB
THerefore the coordinates of P are ((-1-1)/2,(-1+4)/2) = (-1, 3/2)
Similary the coordinates of Q , R and S are (2,4),(5, 3/2), and (2, -1) respectilvely
Length of PQ =`sqrt((-1-2)^2 + (3/2-4)^2) =sqrt(9+25/4)= sqrt(61/4)`
Length of QR =`sqrt((2-5)^2 + (4-3/2)^2) =sqrt(9+25/4)= sqrt(61/4)`
Length of RS =`sqrt((5-2)^2 + (3/2+1)^2) =sqrt(9+25/4)= sqrt(61/4)`
Length of SP =`sqrt((2+1)^2 + (-1-3/2)^2) =sqrt(9+25/4)= sqrt(61/4)`
Length of PR =`sqrt((-1-5)^2 + (3/2-3/2)^2) = 6`
Length of QS = `sqrt((2-2)^2 + (4+1)^2) = 5`
It can be observed that all sides of the given quadrilateral are of the same measure. However, the diagonals are of different lengths. Therefore, PQRS is a rhombus.
APPEARS IN
संबंधित प्रश्न
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
Prove that the points A(2, 4), b(2, 6) and (2 +`sqrt(3)` ,5) are the vertices of an equilateral triangle
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
Find the value of y for which the points A(-3, 9), B(2,y) and C(4,-5) are collinear.
Prove that the points A (a,0), B( 0,b) and C (1,1) are collinear, if `( 1/a+1/b) =1`.
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
If area of a triangular piece of cardboard is 90 cm2, then the length of altitude corresponding to 20 cm long base is ______ cm.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
