Advertisements
Advertisements
प्रश्न
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
पर्याय
14 cm
13 cm
12 cm
11 cm
उत्तर
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is 13 cm.
Explanation:
Given, area of a right-angled triangle = 30 cm2
and smallest side i.e. base = 5 cm
We know that,
Area of right angled triangle = `1/2` × Base × Height
∴ 30 = `1/2` × 5 × Height
⇒ Height = `(30 xx 2)/5`
⇒ Height = 12 cm
Now, according to Pythagoras theorem,
(Hypotenuse)2 = (Perpendicular)2 + (Base)2
⇒ (Hypotenuse)2 = (12)2 + (5)2 ......[∵ Height = Percendicular]
⇒ (Hypotenuse)2 = 144 + 25
⇒ (Hypotenuse)2 = 169
⇒ Hypotenuse = `sqrt(169)`
⇒ Hypotenuse = 13 cm
APPEARS IN
संबंधित प्रश्न
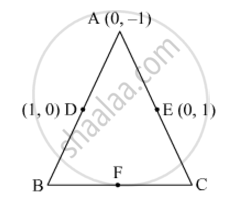
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear
The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
Area of triangle MNO in the figure is ______.