Advertisements
Advertisements
प्रश्न
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is ______.

पर्याय
4.8 cm
3.6 cm
2.4 cm
1.2 cm
उत्तर
In the given figure, ΔMNO is a right-angled triangle. Its legs are 6 cm and 8 cm long. Length of perpendicular NP on the side MO is 4.8 cm.
Explanation:

Given, ΔMNO is a right angled triangle.
So, according to Pythagoras theorem,
MO2 = MN2 + NO2
= 62 + 82
= 36 + 64
⇒ MO2 = 100
⇒ MO = `sqrt(100)`
⇒ MO = 10 cm
∴ Area of ΔMNO = `1/2` × Base × Height
⇒ `1/2` × MN × NO = `1/2` × MO × NP
⇒ `1/2` × 6 × 8 = `1/2` × 10 × NP
⇒ NP = `24/5`
⇒ NP = 4.8 cm
APPEARS IN
संबंधित प्रश्न
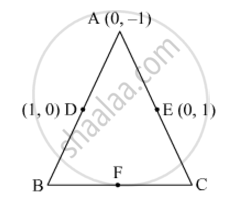
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
If G(-2, 1) is the centroid of a ΔABC and two of its vertices are A(1, -6) and B(-5, 2) , find the third vertex of the triangle.
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
Find the value of y for which the points A(-3, 9), B(2,y) and C(4,-5) are collinear.
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
