Question

A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.

Answer 1

Let ABCD is a rectangular plot having a measurement of 40 m long and 15 m front.

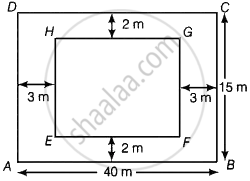
∴ Length of inner-rectangle, EF = 40 – 3 – 3 = 34 m

And breadth of inner-rectangle, FG = 15 – 2 – 2 = 11 m

∴ Another rectangle EFGH will be formed inside the rectangle ABCD

∴ Area of inner-rectangle, EFGH = Length × Breadth  

= EF × FG  ...[∴ Area of a rectangle = length × breadth]

= 34 × 11

= 374 m²  

Hence, the largest area where the house can be constructed in 374 m².