Advertisements
Advertisements
Question
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
Solution
Let ABCD is a rectangular plot having a measurement of 40 m long and 15 m front.
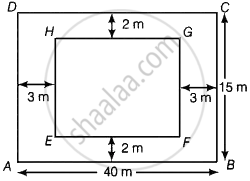
∴ Length of inner-rectangle, EF = 40 – 3 – 3 = 34 m
And breadth of inner-rectangle, FG = 15 – 2 – 2 = 11 m
∴ Another rectangle EFGH will be formed inside the rectangle ABCD
∴ Area of inner-rectangle, EFGH = Length × Breadth
= EF × FG ...[∴ Area of a rectangle = length × breadth]
= 34 × 11
= 374 m2
Hence, the largest area where the house can be constructed in 374 m2.
APPEARS IN
RELATED QUESTIONS
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a+b=1, find the value of a and b.
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:
Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
