Advertisements
Advertisements
Question
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Solution

Let the vertices of the quadrilateral be A ( - 4, - 2), B ( - 3, - 5), C (3, - 2), and D (2, 3). Join AC to form two triangles ΔABC and ΔACD.
Area of a triangle =`1/2 {x_1 (y_2 - y_3) + x_2 (y_3 - y_1) + x_3 (y_1 - y_2)}`
Area of ΔABC = `1/2 [(-4) {(-5) - (-2)} + (-3) {(-2) - (-2)} + 3 {(-2) - (-5)}]`
= `1/2 (12+0+9)`
= 21/2 square units
Area of ΔACD = `1/2 [(-4) {(-2) - (3)} + 3{(3) - (-2)} + 2 {(-2) - (-2)}]`
= `1/2 (20+15+0)`
= 35/2 square units
Area of ☐ABCD = Area of ΔABC + Area of ΔACD
=`(21/2 + 35/2)` square units = 28 square units
APPEARS IN
RELATED QUESTIONS
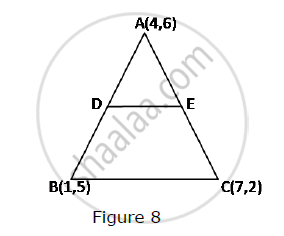
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
If G(-2, 1) is the centroid of a ΔABC and two of its vertices are A(1, -6) and B(-5, 2) , find the third vertex of the triangle.
For what value of x are the points A(-3, 12), B(7, 6) and C(x, 9) collinear.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
Area of a triangle = `1/2` base × ______.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
