Advertisements
Advertisements
Question
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
Solution
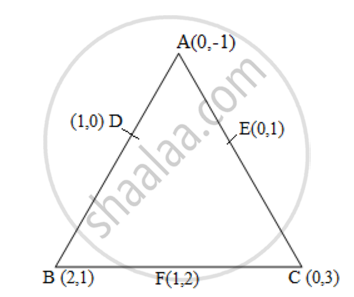
Let the vertices of the triangle be A (0, -1), B (2, 1), C (0, 3).
Let D, E, F be the mid-points of the sides of this triangle. Coordinates of D, E, and F are given by
= 1/2 {8} = 4 square units
APPEARS IN
RELATED QUESTIONS
If the points P(–3, 9), Q(a, b) and R(4, – 5) are collinear and a + b = 1, find the values of a and b.
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
Find values of k if area of triangle is 4 square units and vertices are (k, 0), (4, 0), (0, 2)
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
