Question

Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle

Answer 1

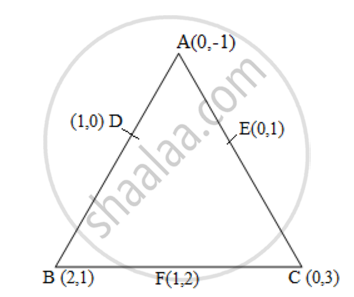
Let the vertices of the triangle be A (0, -1), B (2, 1), C (0, 3).

Let D, E, F be the mid-points of the sides of this triangle. Coordinates of D, E, and F are given by

D = (0+2/2 , -1+1/2) = (1,0)

 

E = (0+0/2 , -3-1/2) = (0,1)

 

F = (2+0/2 , 1+3/2) = (1,2)

 

Area of a triangle = 1/2 {x₁ (y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂)}

 

Area of ΔDEF = 1/2 {1(2-1) + 1(1-0) + 0(0-2)}

                        = 1/2 (1+1) = 1 square units

 

Area of ΔABC = 1/2 [0(1-3) + 2{3-(-1)} + 0(-1-1)]
                         = 1/2 {8} = 4 square units

 

Therefore, the required ratio is 1:4.