Advertisements
Advertisements
प्रश्न
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
उत्तर
For collinear points, area of triangle formed by them is zero.
Therefore, for points (8, 1), (k, - 4), and (2, - 5), area = 0
`1/2 [8 { -4- (-5)} + k{(-5)-(1)} + 2{1 -(-4)}] = 0`
8 - 6k + 10 = 0
6k = 18
k = 3
APPEARS IN
संबंधित प्रश्न
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
Find values of k if area of triangle is 4 square units and vertices are (k, 0), (4, 0), (0, 2)
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
For what value of a point (a, 1), (1, -1) and (11, 4) are collinear?
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
Find the area of the triangle whose vertices are (-2, 6), (3, -6), and (1, 5).
Points A(–6, 10), B(–4, 6) and C(3, –8) are collinear such that AB = `2/9` AC.
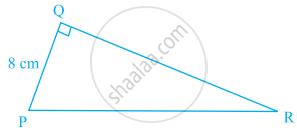
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.