Advertisements
Advertisements
प्रश्न
Find values of k if area of triangle is 4 square units and vertices are (k, 0), (4, 0), (0, 2)
उत्तर
Area of a triangle = `1/2 abs ((x_1,y_1,1),(x_2,y_2,1),(x_3,y_3,1))`
`=> 1/2 abs ((k,0,1),(4,0,1),(0,2,1)) = pm 4`
`=> abs ((k,0,1),(4,0,1),(0,2,1)) = pm 8`
`=> (-2) abs ((k, 1),(4,1)) = pm 8 ` ...[On expanding with respect toC2]
`=> k - 4`
= `pm 4`
`=> "k" = 0, 8`
APPEARS IN
संबंधित प्रश्न
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
Prove that the points (2, – 2), (–3, 8) and (–1, 4) are collinear
Find the area of the triangle whose vertices are: (–5, –1), (3, –5), (5, 2)
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
Find equation of line joining (1, 2) and (3, 6) using the determinant.
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y = x + 3. Find the third vertex.
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
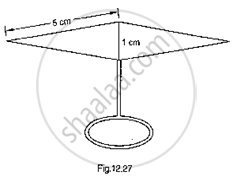
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
If G(-2, 1) is the centroid of a ΔABC and two of its vertices are A(1, -6) and B(-5, 2) , find the third vertex of the triangle.
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
For what value of k(k>0) is the area of the triangle with vertices (-2, 5), (k, -4) and (2k+1, 10) equal to 53 square units?
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
Show that the following points are collinear:
A(8,1), B(3, -4) and C(2, -5)
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
Show that the ∆ABC is an isosceles triangle if the determinant
Δ = `[(1, 1, 1),(1 + cos"A", 1 + cos"B", 1 + cos"C"),(cos^2"A" + cos"A", cos^2"B" + cos"B", cos^2"C" + cos"C")]` = 0
The area of a triangle with vertices (–3, 0), (3, 0) and (0, k) is 9 sq.units. The value of k will be ______.
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
Find the area of the triangle whose vertices are (-2, 6), (3, -6), and (1, 5).
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
Find the value of m if the points (5, 1), (–2, –3) and (8, 2m) are collinear.
If `D((-1)/2, 5/2), E(7, 3)` and `F(7/2, 7/2)` are the midpoints of sides of ∆ABC, find the area of the ∆ABC.
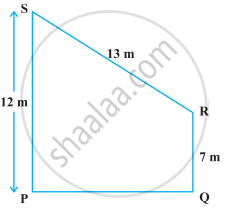
Find the area of the trapezium PQRS with height PQ given in the following figure.
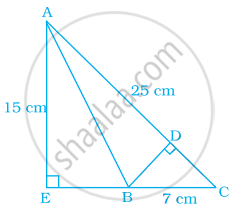
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.