Advertisements
Advertisements
प्रश्न
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
उत्तर
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = 0.
Explanation:
Apply R2 → R2 – R1, R3 → R3 – R1.
APPEARS IN
संबंधित प्रश्न
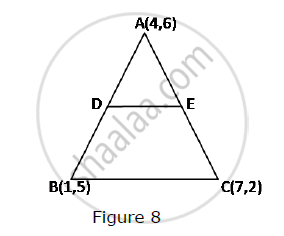
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
If P(–5, –3), Q(–4, –6), R(2, –3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
The vertices of a ΔABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that `(AD)/(AB) = (AE)/(AC) = 1/4`Calculate the area of the ΔADE and compare it with the area of ΔABC. (Recall Converse of basic proportionality theorem and Theorem 6.6 related to ratio of areas of two similar triangles)
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
Find values of k if area of triangle is 4 square units and vertices are (k, 0), (4, 0), (0, 2)
Find the area of the following triangle:

ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
Show that the points are the vertices of an isosceles right triangle.
If G(-2, 1) is the centroid of a ΔABC and two of its vertices are A(1, -6) and B(-5, 2) , find the third vertex of the triangle.
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
Find the area of the following triangle:

The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
If the points (a1, b1), (a2, b2) and(a1 + a2, b1 + b2) are collinear, then ____________.
Let `Delta = abs (("x", "y", "z"),("x"^2, "y"^2, "z"^2),("x"^3, "y"^3, "z"^3)),` then the value of `Delta` is ____________.
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
Find the coordinates of the point Q on the x-axis which lies on the perpendicular bisector of the line segment joining the points A(–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
Find the value of m if the points (5, 1), (–2, –3) and (8, 2m) are collinear.
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 15 cm | 154.5 cm2 |
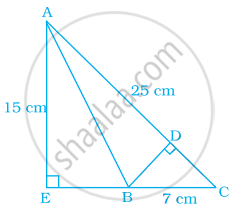
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
