Advertisements
Advertisements
प्रश्न
Find the area of the following triangle:

उत्तर
Area of triangle = `1/2 xx "Base" xx "Height"`
Base = 5 cm,
Height = 3.2 cm
Area = `1/2 xx 5 xx 3.2`
= 8 cm2
APPEARS IN
संबंधित प्रश्न
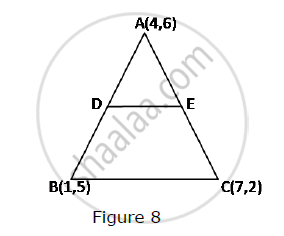
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
Find a relation between x and y, if the points A(2, 1), B(x, y) and C(7,5) are collinear.
Find a relation between x and y, if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Using integration, find the area of the triangle whose vertices are (2, 3), (3, 5) and (4, 4).
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
If the points A(1, 2), O(0, 0) and C(a, b) are collinear, then ______.
