Advertisements
Advertisements
प्रश्न
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
उत्तर
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = 0.
Explanation:
Apply R2 → R2 – R1, R3 → R3 – R1.
APPEARS IN
संबंधित प्रश्न
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
Find equation of line joining (1, 2) and (3, 6) using the determinant.
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
ΔABC is right angled at A (see the given figure). AD is perpendicular to BC. If AB = 5 cm, BC = 13 cm and AC = 12 cm, Find the area of ΔABC. Also find the length of AD.

If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Show that the following sets of points are collinear.
(2, 5), (4, 6) and (8, 8)
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if `1/a+1/b=1`
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
Show that the points are the vertices of an isosceles right triangle.
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
Find the value of y for which the points A(-3, 9), B(2,y) and C(4,-5) are collinear.
Find a relation between x and y, if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.
Find the value(s) of p for which the points (3p + 1, p), (p + 2, p – 5) and (p + 1, –p) are collinear ?
Find the value of p for which the points (−5, 1), (1, p) and (4, −2) are collinear.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ∆ADE.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
Find the values of k if the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear.
The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the following figure. If the area of the trapezium PQCD is `5/6` th part of the area of the rectangle, find the lengths QC and PD.

Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

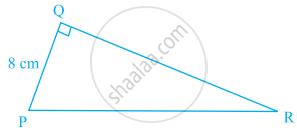
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.
Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
