Advertisements
Advertisements
प्रश्न
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
उत्तर
Let `A(x_1,y_1) = A(2,1), B(x_2, y_2) = B(3,-2)` and `C(x_3,y_3) = C(7/2,y)`
Now
Area(ΔABC) =`1/2|x_1(y_2 - y_3) + x_2(y_3-y_1) + x_3(y_1 - y_2)|`
`=>5 = 1/2|2(-2-y) + 3(y - 1) + 7/2(1+2)|`
`=> 10 = |-4-2y+3y - 3 + 21/2|`
`=>10 = |y + 7/2|`
`=> 10 = y + 7/2` or `-10 = y + 7/2`
`=> y = 13/2` or `y = (-27)/2`
Hence `y = 13/2 or (-27)/2`
APPEARS IN
संबंधित प्रश्न
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
Find the area of the quadrilateral ABCD whose vertices are respectively A(1, 1), B(7, –3), C(12, 2) and D(7, 21).
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
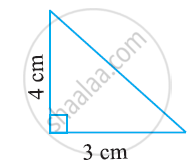
Find the area of the following triangle:
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Prove that the points (a, b), (a1, b1) and (a −a1, b −b1) are collinear if ab1 = a1b.
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle ?
Show that ∆ ABC with vertices A (–2, 0), B (0, 2) and C (2, 0) is similar to ∆ DEF with vertices D (–4, 0), F (4, 0) and E (0, 4) ?
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

