Advertisements
Advertisements
प्रश्न
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
उत्तर
GIVEN: The vertices of triangle ABC are A (−2, 1) and B (5, 4) and C (2, −3)
TO FIND: The area of triangle ABC and length if the altitude through A
PROOF: We know area of triangle formed by three points (x1,y1),(x2,y2)and (x3,y3)is given
by Δ `=1/2[x_1(y_1-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2) `
NOW AREA OF ΔABC
Taking three point A(-2,1) and B(5,4) and C(2,-3)
Area (ΔABC)`=1/2[{-8-15+2}-{5+8+6}]`
`=1/2[{-21}-{19}]`
`=1/2[{-40}]`
`=1/2(40)`
`=20`
WE HAVE
`BC=sqrt((5-2)^2+(4+3)^2)`
`BC=sqrt((3)^2+(7)^2)`
`BC =sqrt(9+49 )`
`BC=sqrt58 `
NOW
Area (ΔABC)`=1/2xxBCxx`ength of altitude though A
20`=1/2xxsqrt 58xx `lenght of altitude through A
Lenght of altitude through A`=40/sqrt58`
APPEARS IN
संबंधित प्रश्न
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
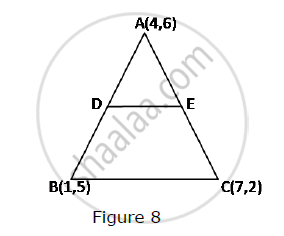
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
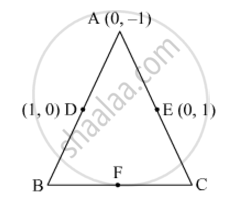
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
In the given figure, if PR = 12 cm, QR = 6 cm and PL = 8 cm, then QM is ______.

Ratio of the area of ∆WXY to the area of ∆WZY is 3:4 in the given figure. If the area of ∆WXZ is 56 cm2 and WY = 8 cm, find the lengths of XY and YZ.

In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

