Advertisements
Advertisements
प्रश्न
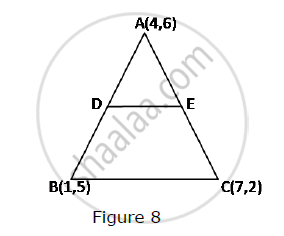
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
उत्तर
`(AD)/(AB)=(AE)/(AC)=1/3`
`:.(AB)/(AD)=(AC)/(AE)=3`
`:.(AD+DB)/(AD)=(AE+EC)/(AE)=3`
`:.1+(DB)/(AD)=1+(EC)/(AE)=3`
`:.(DB)/(AD)=(EC)/(AE)=2`
`:.(AD)/(DB)=(AE)/(EC)=1/2`
∴ AD:DB = AE :EC = 1: 2
So, D and E divide AB and AC respectively in the ratio 1:2.
So the coordinates of D and E are
`((1+8)/(1+2),(5+12)/(1+2))=(3,17/3) `
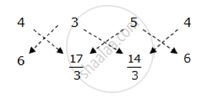
Area of ΔADE
`=1/2|(4xx17/3+3xx14/3+5xx6)-(3xx6+5xx17/3+4xx14/3)|`
`=1/2|(68/3+14+30)-(18+85/3+56/3)|`
`=1/2|((68+42+90)/3)-((54+85+56)/3)|`
`=1/2|(200/3)-(195/3)|`
`=1/2xx5/3`
`=5/6 `
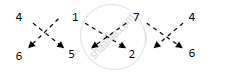
Area of ΔABC
`=1/2|(4xx5+1xx2+7xx6)-(1xx6+7xx5+4xx2)|`
`=1/2|(20+2+42)-(6+35+8)|`
`=1/2|64-49|`
`=15/2`
`:.(`
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Find values of k if area of triangle is 4 square units and vertices are (k, 0), (4, 0), (0, 2)
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
Find the area of the following triangle:

In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm. 
Find:
(i) the area of the ∆PQR
(ii) QM.
In the given figure, if PR = 12 cm, QR = 6 cm and PL = 8 cm, then QM is ______.

Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
