Advertisements
Advertisements
प्रश्न
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
उत्तर
Area of the triangle passing through the vertices `(x_1,y_1),(x_2,y_2),(x_3,y_3)`
`Delta = 1/2 abs ((x_1,y_1,1),(x_2,y_2,1),(x_3,y_3,1))`
Area of the required triangle
`Delta = 1/2 abs((1,0,1),(6,0,1),(4,3,1))`
`=1/2 [1 (0 - 3) - 0 (6 - 4) + 1 (18 - 0)] `
`= 1/2 [-3 + 18]`
`= 15/2`
= 7.5 sq. units.
APPEARS IN
संबंधित प्रश्न
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and (5k – 1, 5k) are collinear.
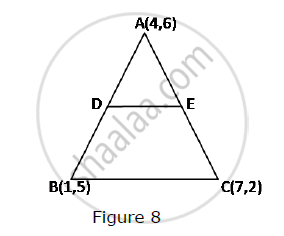
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
If the points A(−2, 1), B(a, b) and C(4, −1) are collinear and a − b = 1, find the values of a and b.
If the points A(−1, −4), B(b, c) and C(5, −1) are collinear and 2b + c = 4, find the values of b and c.
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
Prove that the points (2a, 4a), (2a, 6a) and `(2a + sqrt3a, 5a)` are the vertices of an equilateral triangle.
Prove that the points (2,3), (-4, -6) and (1, 3/2) do not form a triangle.
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Show that the points are the vertices of an isosceles right triangle.
Prove that the points A(2, 4), b(2, 6) and (2 +`sqrt(3)` ,5) are the vertices of an equilateral triangle
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
For what value of y, are the points P(1, 4), Q(3,y) and R(-3, 16) are collinear ?
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear ?
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm. 
Find:
(i) the area of the ∆PQR
(ii) QM.
If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 5 feet | ? | 20 sq.feet |
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
The points (1,1), (-2, 7) and (3, -3) are ______.
The points (0, 5), (0, –9) and (3, 6) are collinear.
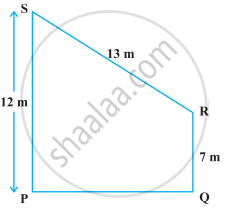
Find the area of the trapezium PQRS with height PQ given in the following figure.
The dimensions of a rectangle ABCD are 51 cm × 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8, is cut off from the rectangle as shown in the following figure. If the area of the trapezium PQCD is `5/6` th part of the area of the rectangle, find the lengths QC and PD.

Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

Area of a triangle = `1/2` base × ______.
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
Triangles having the same base have equal area.
In the given figure, area of ΔPQR is 20 cm2 and area of ΔPQS is 44 cm2. Find the length RS, if PQ is perpendicular to QS and QR is 5 cm.

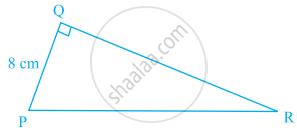
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.