Advertisements
Advertisements
प्रश्न
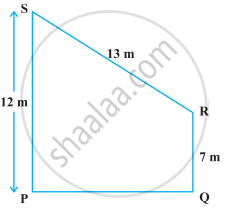
Find the area of the trapezium PQRS with height PQ given in the following figure.
उत्तर
We have, trapezium PQRS, in which draw a line RT perpendicular to PS.
Where, side, ST = PS – TP = 12 – 7 = 5 m. ...[∵ TP = PQ = 7 m]
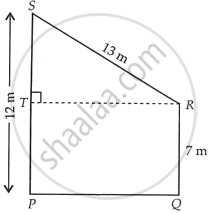
In right angled ΔSTR,
(SR)2 = (ST)2 + (TR)2 ...[By using Pythagoras theorem]
⇒ (13)2 = (5)2 + (TR)2
⇒ (TR)2 = 169 – 25
⇒ (TR)2 = 144
∴ TR = 12 m ...[Taking positive square root because length is always positive]
Now, area of ΔSTR = `1/2 xx TR xx TS` ...[∵ Area of triangle = `1/2` (base × height)]
= `1/2 xx 12 xx 5`
= 30 m2
Now, area of rectangle PQRT = PQ × RQ ...[∵ Area of a rectangle = length × breadth]
= 12 × 7
= 84 m2 ...[∵ PQ = TR = 12 m]
∴ Area of trapezium = Area of ΔSTR + Area of rectangle PQRT
= 30 + 84
= 114 m2
Hence, the area of trapezium is 114 m2.
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
Find the area of the quadrilateral ABCD whose vertices are respectively A(1, 1), B(7, –3), C(12, 2) and D(7, 21).
Find equation of line joining (3, 1) and (9, 3) using determinant.
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:
Find the area of the following triangle:

The points (1,1), (-2, 7) and (3, -3) are ______.
Find the missing value:
| Base | Height | Area of Triangle |
| ______ | 31.4 mm | 1256 mm2 |
